➡ A solução para você consegue descobrir a idade deste matemático morto?
Primeiro, vamos resolver isso usando nossas habilidades básicas de fração. Depois de apreciar o poema, podemos dividir tudo em uma soma básica:
Vida de Diofanto = Infância + Bigodes + Antes do Casamento + 5 + Vida do Filho + 4…
Cada um desses segmentos pode ser visto como um valor fracionário de A, a idade final de Diofanto. Substituindo as dicas do poema nos dá uma nova equação.

Limpar essa equação não demora muito. Só precisamos encontrar um denominador comum e adicionar termos semelhantes.
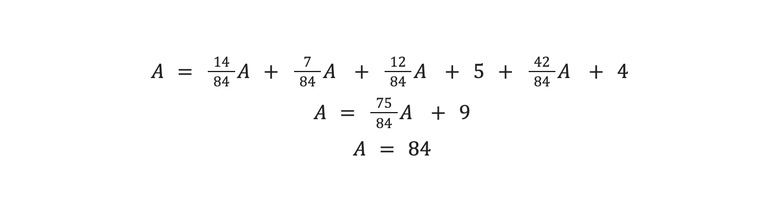
Então, frações nos dizem que a solução é 84. Mas você pode estar se perguntando por que 84 aparece no problema antes que a equação seja totalmente resolvida. Isso porque o problema em si é uma equação diofantina! Podemos resolver todo o problema com apenas números inteiros e um pouco de lógica.
Considere o que sabemos sobre o problema e a possível solução: sabemos que existe uma idade mágica A que é um múltiplo de 6, porque a “infância” dura exatamente um sexto dessa idade. Não só é um múltiplo de 6, mas também 12, 7 e 2. Há um conjunto infinito de valores que são múltiplos desses quatro números, mas a realidade nos diz que há apenas uma pequena janela de idades potenciais que Diofanto pode ter alcançado .
O mínimo múltiplo comum de 6, 12, 7 e 2? É 84. O próximo múltiplo potencial desses números é 168 – bem fora dos limites da expectativa de vida humana na Grécia antiga!










